Chapter 16. Collections

We all behave like Maxwell’s demon. Organisms organize. In everyday experience lies the reason sober physicists across two centuries kept this cartoon fantasy alive. We sort the mail, build sand castles, solve jigsaw puzzles, separate wheat from chaff, rearrange chess pieces, collect stamps, alphabetize books, create symmetry, compose sonnets and sonatas, and put our rooms in order, and all this we do requires no great energy, as long as we can apply intelligence.

James Gleick, The Information: A History, a Theory, a Flood

The Rust standard library contains several collections, generic types for storing data in memory. We’ve already been using collections, such as Vec and HashMap, throughout this book. In this chapter, we’ll cover the methods of these two types in detail, along with the other half-dozen standard collections. Before we begin, let’s address a few systematic differences between Rust’s collections and those in other languages.

First, moves and borrowing are everywhere. Rust uses moves to avoid deep-copying values. That’s why the method Vec<T>::push(item) takes its argument by value, not by reference. The value is moved into the vector. The diagrams in Chapter 4 show how this works out in practice: pushing a Rust String to a Vec<String> is quick, because Rust doesn’t have to copy the string’s character data, and ownership of the string is always clear.

Second, Rust doesn’t have invalidation errors—the kind of dangling-pointer bug where a collection is resized, or otherwise changed, while the program is holding a pointer to data inside it. Invalidation errors are another source of undefined behavior in C++, and they cause the occasional ConcurrentModificationException even in memory-safe languages. Rust’s borrow checker rules them out at compile time.

Finally, Rust does not have null, so we’ll see Options in places where other languages would use null.

Apart from these differences, Rust’s collections are about what you’d expect. If you’re an experienced programmer in a hurry, you can skim here, but don’t miss “Entries”.

Overview

Table 16-1 shows Rust’s eight standard collections. All of them are generic types.

Table 16-1. Summary of the standard collections
Collection Description Similar collection type in...
C++ Java Python
Vec<T> Growable array vector ArrayList list
VecDeque<T> Double-ended queue
(growable ring buffer)		 deque ArrayDeque collections​.deque
LinkedList<T> Doubly linked list list LinkedList —
BinaryHeap<T>
where T: Ord		 Max heap priority_queue PriorityQueue heapq
HashMap<K, V>
where K: Eq + Hash		 Key-value hash table unordered_map HashMap dict
BTreeMap<K, V>
where K: Ord		 Sorted key-value table map TreeMap —
HashSet<T>
where T: Eq + Hash		 Unordered, hash-based set unordered_set HashSet set
BTreeSet<T>
where T: Ord		 Sorted set set TreeSet —

Vec<T>, HashMap<K, V>, and HashSet<T> are the most generally useful collection types. The rest have niche uses. This chapter discusses each collection type in turn:

Vec<T>
A growable, heap-allocated array of values of type T. About half of this chapter is dedicated to Vec and its many useful methods.
VecDeque<T>
Like Vec<T>, but better for use as a first-in-first-out queue. It supports efficiently adding and removing values at the front of the list as well as the back. This comes at the cost of making all other operations slightly slower.
BinaryHeap<T>
A priority queue. The values in a BinaryHeap are organized so that it’s always efficient to find and remove the maximum value.
HashMap<K, V>
A table of key-value pairs. Looking up a value by its key is fast. The entries are stored in an arbitrary order.
BTreeMap<K, V>
Like HashMap<K, V>, but it keeps the entries sorted by key. A BTreeMap<String, i32> stores its entries in String comparison order. Unless you need the entries to stay sorted, a HashMap is faster.
HashSet<T>
A set of values of type T. Adding and removing values is fast, and it’s fast to ask whether a given value is in the set or not.
BTreeSet<T>
Like HashSet<T>, but it keeps the elements sorted by value. Again, unless you need the data sorted, a HashSet is faster.

Because LinkedList is rarely used (and there are better alternatives, both in performance and interface, for most use cases), we do not describe it here.

Vec<T>

We’ll assume some familiarity with Vec, since we’ve been using it throughout the book. For an introduction, see “Vectors”. Here we’ll finally describe its methods and its inner workings in depth.

The easiest way to create a vector is to use the vec! macro:

// Create an empty vector
let mut numbers: Vec<i32> = vec![];

// Create a vector with given contents
let words = vec!["step", "on", "no", "pets"];
let mut buffer = vec![0u8; 1024];  // 1024 zeroed-out bytes

As described in Chapter 4, a vector has three fields: the length, the capacity, and a pointer to a heap allocation where the elements are stored. Figure 16-1 shows how the preceding vectors would appear in memory. The empty vector, numbers, initially has a capacity of 0. No heap memory is allocated for it until the first element is added.

Like all collections, Vec implements std::iter::FromIterator, so you can create a vector from any iterator using the iterator’s .collect() method, as described in “Building Collections: collect and FromIterator”:

// Convert another collection to a vector.
let my_vec = my_set.into_iter().collect::<Vec<String>>();
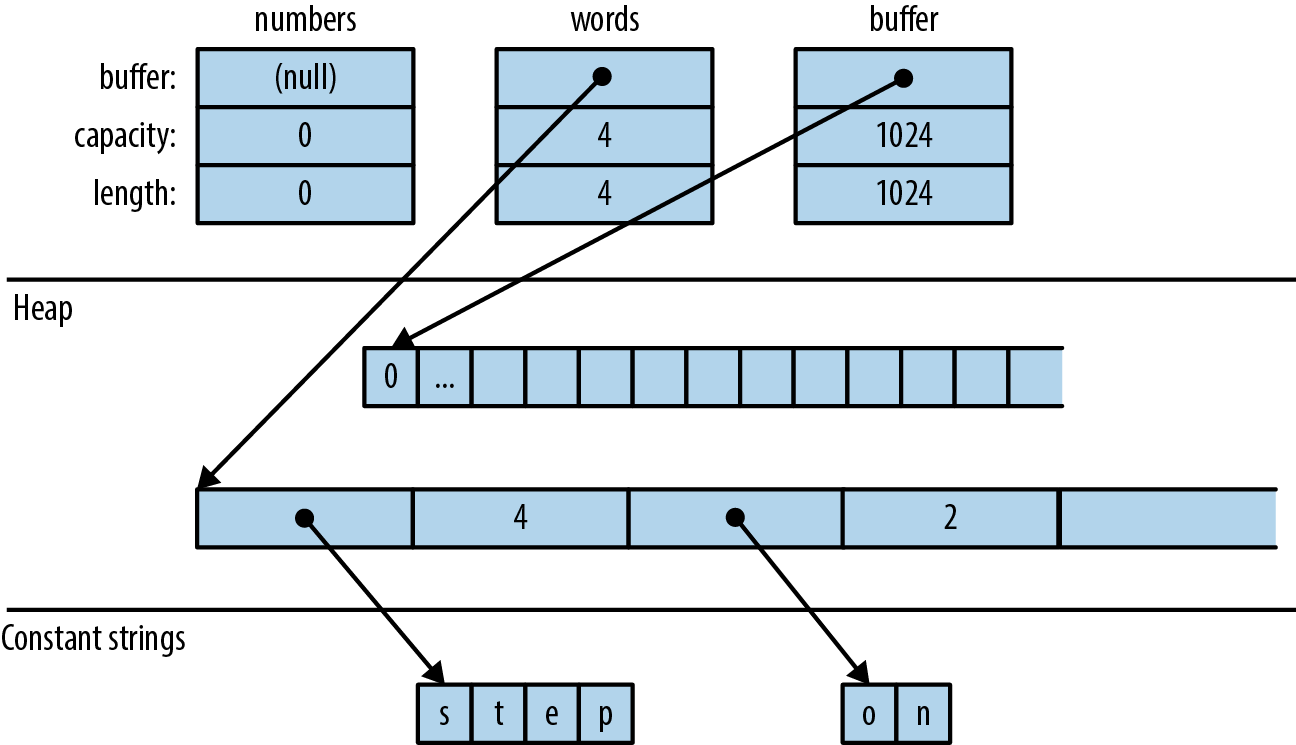
(Each vector has three fields: a buffer pointer, the capacity, and the length. The buffer pointer of the "numbers" vector is null, and its capacity is zero. Each of the other buffer pointers points to a heap-allocated array and has a capacity equal to its length.)
Figure 16-1. Vector layout in memory: each element of words is a &str value consisting of a pointer and a length

Accessing Elements

Getting elements of an array, slice, or vector by index is straightforward:

// Get a reference to an element
let first_line = &lines[0];

// Get a copy of an element
let fifth_number = numbers[4];       // requires Copy
let second_line = lines[1].clone();  // requires Clone

// Get a reference to a slice
let my_ref = &buffer[4..12];

// Get a copy of a slice
let my_copy = buffer[4..12].to_vec();  // requires Clone

All of these forms panic if an index is out of bounds.

Rust is picky about numeric types, and it makes no exceptions for vectors. Vector lengths and indices are of type usize. Trying to use a u32, u64, or isize as a vector index is an error. You can use an n as usize cast to convert as needed; see “Type Casts”.

Several methods provide easy access to particular elements of a vector or slice (note that all slice methods are available on arrays and vectors too):

slice.first()

Returns a reference to the first element of slice, if any.

The return type is Option<&T>, so the return value is None if slice is empty and Some(&slice[0]) if it’s not empty:

if let Some(item) = v.first() {
    println!("We got one! {}", item);
}
slice.last()
Similar but returns a reference to the last element.
slice.get(index)

Returns Some reference to slice[index], if it exists. If slice has fewer than index+1 elements, this returns None:

let slice = [0, 1, 2, 3];
assert_eq!(slice.get(2), Some(&2));
assert_eq!(slice.get(4), None);
slice.first_mut(), slice.last_mut(), slice.get_mut(index)

Variations of the preceding that borrow mut references:

let mut slice = [0, 1, 2, 3];
{
    let last = slice.last_mut().unwrap();   // type of last: &mut i32
    assert_eq!(*last, 3);
    *last = 100;
}
assert_eq!(slice, [0, 1, 2, 100]);

Because returning a T by value would mean moving it, methods that access elements in place typically return those elements by reference.

An exception is the .to_vec() method, which makes copies:

slice.to_vec()

Clones a whole slice, returning a new vector:

let v = [1, 2, 3, 4, 5, 6, 7, 8, 9];
assert_eq!(v.to_vec(),
           vec![1, 2, 3, 4, 5, 6, 7, 8, 9]);
assert_eq!(v[0..6].to_vec(),
           vec![1, 2, 3, 4, 5, 6]);

This method is available only if the elements are cloneable, that is, where T: Clone.

Iteration

Vectors and slices are iterable, either by value or by reference, following the pattern described in “IntoIterator Implementations”:

  • Iterating over a Vec<T> produces items of type T. The elements are moved out of the vector one by one, consuming it.

  • Iterating over a value of type &[T; N], &[T], or &Vec<T>—that is, a reference to an array, slice, or vector—produces items of type &T, references to the individual elements, which are not moved.

  • Iterating over a value of type &mut [T; N], &mut [T], or &mut Vec<T> produces items of type &mut T.

Arrays, slices, and vectors also have .iter() and .iter_mut() methods (described in “iter and iter_mut Methods”) for creating iterators that produce references to their elements.

We’ll cover some fancier ways to iterate over a slice in “Splitting”.

Growing and Shrinking Vectors

The length of an array, slice, or vector is the number of elements it contains:

slice.len()
Returns a slice’s length, as a usize.
slice.is_empty()
Is true if slice contains no elements (that is, slice.len() == 0).

The remaining methods in this section are about growing and shrinking vectors. They are not present on arrays and slices, which can’t be resized once created.

All of a vector’s elements are stored in a contiguous, heap-allocated chunk of memory. The capacity of a vector is the maximum number of elements that would fit in this chunk. Vec normally manages the capacity for you, automatically allocating a larger buffer and moving the elements into it when more space is needed. There are also a few methods for managing capacity explicitly:

Vec::with_capacity(n)
Creates a new, empty vector with capacity n.
vec.capacity()
Returns vec’s capacity, as a usize. It’s always true that vec.capacity() >= vec.len().
vec.reserve(n)
Makes sure the vector has at least enough spare capacity for n more elements: that is, vec.capacity() is at least vec.len() + n. If there’s already enough room, this does nothing. If not, this allocates a larger buffer and moves the vector’s contents into it.
vec.reserve_exact(n)
Like vec.reserve(n), but tells vec not to allocate any extra capacity for future growth, beyond n. Afterward, vec.capacity() is exactly vec.len() + n.
vec.shrink_to_fit()
Tries to free up the extra memory if vec.capacity() is greater than vec.len().

Vec<T> has many methods that add or remove elements, changing the vector’s length. Each of these takes its self argument by mut reference.

These two methods add or remove a single value at the end of a vector:

vec.push(value)
Adds the given value to the end of vec.
vec.pop()
Removes and returns the last element. The return type is Option<T>. This returns Some(x) if the popped element is x and None if the vector was already empty.

Note that .push() takes its argument by value, not by reference. Likewise, .pop() returns the popped value, not a reference. The same is true of most of the remaining methods in this section. They move values in and out of vectors.

These two methods add or remove a value anywhere in a vector:

vec.insert(index, value)

Inserts the given value at vec[index], sliding any existing values in vec[index..] one spot to the right to make room.

Panics if index > vec.len().

vec.remove(index)

Removes and returns vec[index], sliding any existing values in vec[index+1..] one spot to the left to close the gap.

Panics if index >= vec.len(), since in that case there is no element vec[index] to remove.

The longer the vector, the slower this operation gets. If you find yourself doing vec.remove(0) a lot, consider using a VecDeque (explained in “VecDeque<T>”) instead of a Vec.

Both .insert() and .remove() are slower the more elements have to be shifted.

Four methods change the length of a vector to a specific value:

vec.resize(new_len, value)
Sets vec’s length to new_len. If this increases vec’s length, copies of value are added to fill the new space. The element type must implement the Clone trait.
vec.resize_with(new_len, closure)
Just like vec.resize, but calls the closure to construct each new element. It can be used with vectors of elements that are not Clone.
vec.truncate(new_len)

Reduces the length of vec to new_len, dropping any elements that were in the range vec[new_len..].

If vec.len() is already less than or equal to new_len, nothing happens.

vec.clear()
Removes all elements from vec. It’s the same as vec.truncate(0).

Four methods add or remove many values at once:

vec.extend(iterable)

Adds all items from the given iterable value at the end of vec, in order. It’s like a multivalue version of .push(). The iterable argument can be anything that implements IntoIterator<Item=T>.

This method is so useful that there’s a standard trait for it, the Extend trait, which all standard collections implement. Unfortunately, this causes rustdoc to lump .extend() with other trait methods in a big pile at the bottom of the generated HTML, so it’s hard to find when you need it. You just have to remember it’s there! See “The Extend Trait” for more.

vec.split_off(index)
Like vec.truncate(index), except that it returns a Vec<T> containing the values removed from the end of vec. It’s like a multivalue version of .pop().
vec.append(&mut vec2)

This moves all elements from vec2 into vec, where vec2 is another vector of type Vec<T>. Afterward, vec2 is empty.

This is like vec.extend(vec2) except that vec2 still exists afterward, with its capacity unaffected.

vec.drain(range)
This removes the range vec[range] from vec and returns an iterator over the removed elements, where range is a range value, like .. or 0..4.

There are also a few oddball methods for selectively removing some of a vector’s elements:

vec.retain(test)

Removes all elements that don’t pass the given test. The test argument is a function or closure that implements FnMut(&T) -> bool. For each element of vec, this calls test(&element), and if it returns false, the element is removed from the vector and dropped.

Apart from performance, this is like writing:

vec = vec.into_iter().filter(test).collect();
vec.dedup()

Drops repeated elements. It’s like the Unix uniq shell utility. It scans vec for places where adjacent elements are equal and drops the extra equal values so that only one is left:

let mut byte_vec = b"Misssssssissippi".to_vec();
byte_vec.dedup();
assert_eq!(&byte_vec, b"Misisipi");

Note that there are still two 's' characters in the output. This method only removes adjacent duplicates. To eliminate all duplicates, you have three options: sort the vector before calling .dedup(), move the data into a set, or (to keep the elements in their original order) use this .retain() trick:

let mut byte_vec = b"Misssssssissippi".to_vec();

let mut seen = HashSet::new();
byte_vec.retain(|r| seen.insert(*r));

assert_eq!(&byte_vec, b"Misp");

This works because .insert() returns false when the set already contains the item we’re inserting.

vec.dedup_by(same)
The same as vec.dedup(), but it uses the function or closure same(&mut elem1, &mut elem2), instead of the == operator, to check whether two elements should be considered equal.
vec.dedup_by_key(key)

The same as vec.dedup(), but it treats two elements as equal if key(&mut elem1) == key(&mut elem2).

For example, if errors is a Vec<Box<dyn Error>>, you can write:

// Remove errors with redundant messages.
errors.dedup_by_key(|err| err.to_string());

Of all the methods covered in this section, only .resize() ever clones values. The others work by moving values from one place to another.

Splitting

It’s easy to get many non-mut references into an array, slice, or vector at once:

let v = vec![0, 1, 2, 3];
let a = &v[i];
let b = &v[j];

let mid = v.len() / 2;
let front_half = &v[..mid];
let back_half = &v[mid..];

Getting multiple mut references is not so easy:

let mut v = vec![0, 1, 2, 3];
let a = &mut v[i];
let b = &mut v[j];  // error: cannot borrow `v` as mutable
                    //        more than once at a time

*a = 6;             // references `a` and `b` get used here,
*b = 7;             // so their lifetimes must overlap

Rust forbids this because if i == j, then a and b would be two mut references to the same integer, in violation of Rust’s safety rules. (See “Sharing Versus Mutation”.)

Rust has several methods that can borrow mut references to two or more parts of an array, slice, or vector at once. Unlike the preceding code, these methods are safe, because by design, they always split the data into nonoverlapping regions. Many of these methods are also handy for working with non-mut slices, so there are mut and non-mut versions of each.

Figure 16-2 illustrates these methods.

(The illustration shows an array of integers and the output of various split methods, using long horizontal bars to represent slice references in the output. The output of the "windows" method looks like steps; the other methods always produce non-overlapping slices, so each method's output is shown as a single bar, broken in various places.)
Figure 16-2. Splitting methods illustrated (note: the little rectangle in the output of slice.split() is an empty slice caused by the two adjacent separators, and rsplitn produces its output in end-to-start order, unlike the others)

None of these methods directly modifies an array, slice, or vector; they merely return new references to parts of the data inside:

slice.iter(), slice.iter_mut()
Produce a reference to each element of slice. We covered them in “Iteration”.
slice.split_at(index), slice.split_at_mut(index)
Break a slice in two, returning a pair. slice.split_at(index) is equivalent to (&slice[..index], &slice[index..]). These methods panic if index is out of bounds.
slice.split_first(), slice.split_first_mut()

Also return a pair: a reference to the first element (slice[0]) and a slice reference to all the rest (slice[1..]).

The return type of .split_first() is Option<(&T, &[T])>; the result is None if slice is empty.

slice.split_last(), slice.split_last_mut()

These are analogous but split off the last element rather than the first.

The return type of .split_last() is Option<(&T, &[T])>.

slice.split(is_sep), slice.split_mut(is_sep)

Split slice into one or more subslices, using the function or closure is_sep to figure out where to split. They return an iterator over the subslices.

As you consume the iterator, it calls is_sep(&element) for each element in the slice. If is_sep(&element) is true, the element is a separator. Separators are not included in any output subslice.

The output always contains at least one subslice, plus one per separator. Empty subslices are included whenever separators appear adjacent to each other or to the ends of slice.

slice.rsplit(is_sep), slice.rsplit_mut(is_sep)
Just like slice and slice_mut, but start at the end of the slice.
slice.splitn(n, is_sep), slice.splitn_mut(n, is_sep)
The same but they produce at most n subslices. After the first n-1 slices are found, is_sep is not called again. The last subslice contains all the remaining elements.
slice.rsplitn(n, is_sep), slice.rsplitn_mut(n, is_sep)
Just like .splitn() and .splitn_mut() except that the slice is scanned in reverse order. That is, these methods split on the last n-1 separators in the slice, rather than the first, and the subslices are produced starting from the end.
slice.chunks(n), slice.chunks_mut(n)
Return an iterator over nonoverlapping subslices of length n. If n doesn’t divide slice.len() exactly, the last chunk will contain fewer than n elements.
slice.rchunks(n), slice.rchunks_mut(n)
Just like slice.chunks and slice.chunks_mut, but start at the end of the slice.
slice.chunks_exact(n), slice.chunks_exact_mut(n)
Return an iterator over nonoverlapping subslices of length n. If n doesn’t divide slice.len(), the last chunk (with less than n elements) is available in the result’s remainder() method.
slice.rchunks_exact(n), slice.rchunks_exact_mut(n)
Just like slice.chunks_exact and slice.chunks_exact_mut, but start at the end of the slice.

There’s one more method for iterating over subslices:

slice.windows(n)

Returns an iterator that behaves like a “sliding window” over the data in slice. It produces subslices that span n consecutive elements of slice. The first value produced is &slice[0..n], the second is &slice[1..n+1], and so on.

If n is greater than the length of slice, then no slices are produced. If n is 0, the method panics.

For example, if days.len() == 31, then we can produce all seven-day spans in days by calling days.windows(7).

A sliding window of size 2 is handy for exploring how a data series changes from one data point to the next:

let changes = daily_high_temperatures
                  .windows(2)             // get adjacent days' temps
                  .map(|w| w[1] - w[0])   // how much did it change?
                  .collect::<Vec<_>>();

Because the subslices overlap, there is no variation of this method that returns mut references.

Sorting and Searching

Slices offer three methods for sorting:

slice.sort()
Sorts the elements into increasing order. This method is present only when the element type implements Ord.
slice.sort_by(cmp)

Sorts the elements of slice using a function or closure cmp to specify the sort order. cmp must implement Fn(&T, &T) -> std::cmp::Ordering.

Hand-implementing cmp is a pain, unless you delegate to a .cmp() method:

students.sort_by(|a, b| a.last_name.cmp(&b.last_name));

To sort by one field, using a second field as a tiebreaker, compare tuples:

students.sort_by(|a, b| {
    let a_key = (&a.last_name, &a.first_name);
    let b_key = (&b.last_name, &b.first_name);
    a_key.cmp(&b_key)
});
slice.sort_by_key(key)

Sorts the elements of slice into increasing order by a sort key, given by the function or closure key. The type of key must implement Fn(&T) -> K where K: Ord.

This is useful when T contains one or more ordered fields, so that it could be sorted multiple ways:

// Sort by grade point average, lowest first.
students.sort_by_key(|s| s.grade_point_average());

Note that these sort-key values are not cached during sorting, so the key function may be called more than n times.

For technical reasons, key(element) can’t return any references borrowed from the element. This won’t work:

students.sort_by_key(|s| &s.last_name);  // error: can't infer lifetime

Rust can’t figure out the lifetimes. But in these cases, it’s easy enough to fall back on .sort_by().

All three methods perform a stable sort.

To sort in reverse order, you can use sort_by with a cmp closure that swaps the two arguments. Taking arguments |b, a| rather than |a, b| effectively produces the opposite order. Or, you can just call the .reverse() method after sorting:

slice.reverse()
Reverses a slice in place.

Once a slice is sorted, it can be efficiently searched:

slice.binary_search(&value), slice.binary_search_by(&value, cmp), slice.binary_search_by_key(&value, key)

All search for value in the given sorted slice. Note that value is passed by reference.

The return type of these methods is Result<usize, usize>. They return Ok(index) if slice[index] equals value under the specified sort order. If there is no such index, then they return Err(insertion_point) such that inserting value at insertion_point would preserve the order.

Of course, a binary search only works if the slice is in fact sorted in the specified order. Otherwise, the results are arbitrary—garbage in, garbage out.

Since f32 and f64 have NaN values, they do not implement Ord and can’t be used directly as keys with the sorting and binary search methods. To get similar methods that work on floating-point data, use the ord_subset crate.

There’s one method for searching a vector that is not sorted:

slice.contains(&value)
Returns true if any element of slice is equal to value. This simply checks each element of the slice until a match is found. Again, value is passed by reference.

To find the location of a value in a slice, like array.indexOf(value) in JavaScript, use an iterator:

slice.iter().position(|x| *x == value)

This returns an Option<usize>.

Comparing Slices

If a type T supports the == and != operators (the PartialEq trait, described in “Equivalence Comparisons”), then arrays [T; N], slices [T], and vectors Vec<T> support them too. Two slices are equal if they’re the same length and their corresponding elements are equal. The same goes for arrays and vectors.

If T supports the operators <, <=, >, and >= (the PartialOrd trait, described in “Ordered Comparisons”), then arrays, slices, and vectors of T do too. Slice comparisons are lexicographical.

Two convenience methods perform common slice comparisons:

slice.starts_with(other)

Returns true if slice starts with a sequence of values that are equal to the elements of the slice other:

assert_eq!([1, 2, 3, 4].starts_with(&[1, 2]), true);
assert_eq!([1, 2, 3, 4].starts_with(&[2, 3]), false);
slice.ends_with(other)

Similar but checks the end of slice:

assert_eq!([1, 2, 3, 4].ends_with(&[3, 4]), true);

Rust Rules Out Invalidation Errors

Most mainstream programming languages have collections and iterators, and they all have some variation on this rule: don’t modify a collection while you’re iterating over it. For example, the Python equivalent of a vector is a list:

my_list = [1, 3, 5, 7, 9]

Suppose we try to remove all values greater than 4 from my_list:

for index, val in enumerate(my_list):
    if val > 4:
        del my_list[index]  # bug: modifying list while iterating

print(my_list)

(The enumerate function is Python’s equivalent of Rust’s .enumerate() method, described in “enumerate”.)

This program, surprisingly, prints [1, 3, 7]. But seven is greater than four. How did that slip through? This is an invalidation error: the program modifies data while iterating over it, invalidating the iterator. In Java, the result would be an exception; in C++ it is undefined behavior. In Python, while the behavior is well-defined, it’s unintuitive: the iterator skips an element. val is never 7.

Let’s try to reproduce this bug in Rust:

fn main() {
    let mut my_vec = vec![1, 3, 5, 7, 9];

    for (index, &val) in my_vec.iter().enumerate() {
        if val > 4 {
            my_vec.remove(index);  // error: can't borrow `my_vec` as mutable
        }
    }
    println!("{:?}", my_vec);
}

Naturally, Rust rejects this program at compile time. When we call my_vec.iter(), it borrows a shared (non-mut) reference to the vector. The reference lives as long as the iterator, to the end of the for loop. We can’t modify the vector by calling my_vec.remove(index) while a non-mut reference exists.

Having an error pointed out to you is nice, but of course, you still need to find a way to get the desired behavior! The easiest fix here is to write:

my_vec.retain(|&val| val <= 4);

Or, you can do what you’d do in Python or any other language: create a new vector using a filter.

VecDeque<T>

Vec supports efficiently adding and removing elements only at the end. When a program needs a place to store values that are “waiting in line,” Vec can be slow.

Rust’s std::collections::VecDeque<T> is a deque (pronounced “deck”), a double-ended queue. It supports efficient add and remove operations at both the front and the back:

deque.push_front(value)
Adds a value at the front of the queue.
deque.push_back(value)
Adds a value at the end. (This method is used much more than .push_front(), because the usual convention for queues is that values are added at the back and removed at the front, like people waiting in a line.)
deque.pop_front()
Removes and returns the front value of the queue, returning an Option<T> that is None if the queue is empty, like vec.pop().
deque.pop_back()
Removes and returns the value at the back, again returning an Option<T>.
deque.front(), deque.back()
Work like vec.first() and vec.last(). They return a reference to the front or back element of the queue. The return value is an Option<&T> that is None if the queue is empty.
deque.front_mut(), deque.back_mut()
Work like vec.first_mut() and vec.last_mut(), returning Option<&mut T>.

The implementation of VecDeque is a ring buffer, as shown in Figure 16-3.

Like a Vec, it has a single heap allocation where elements are stored. Unlike Vec, the data does not always start at the beginning of this region, and it can “wrap around” the end, as shown. The elements of this deque, in order, are ['A', 'B', 'C', 'D', 'E']. VecDeque has private fields, labeled start and stop in the figure, that it uses to remember where in the buffer the data begins and ends.

Adding a value to the queue, on either end, means claiming one of the unused slots, illustrated as the darker blocks, wrapping around or allocating a bigger chunk of memory if needed.

VecDeque manages wrapping, so you don’t have to think about it. Figure 16-3 is a behind-the-scenes view of how Rust makes .pop_front() fast.

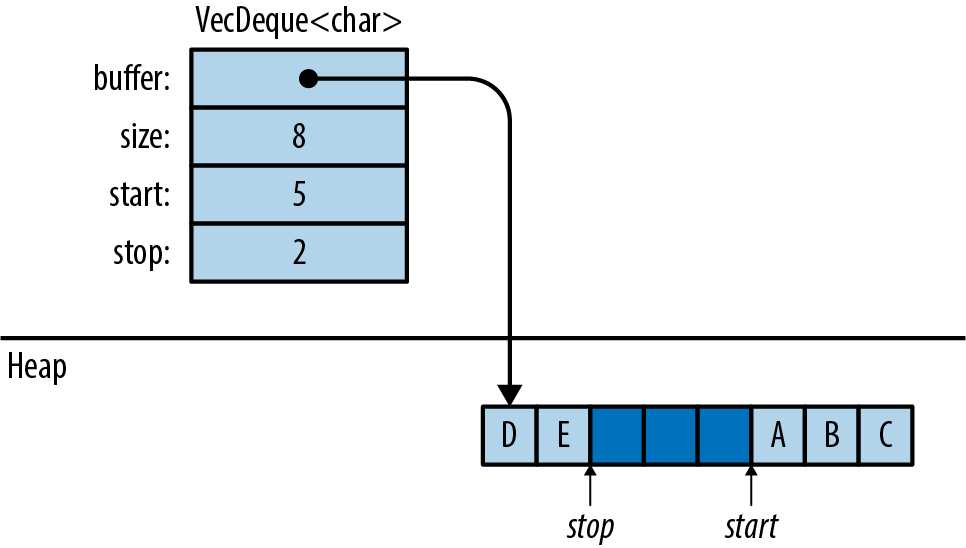
(An illustration of a VecDeque of characters. The deque's heap storage contains the characters 'D' and 'E', then a gap of three char-sized slots, then the characters 'A', 'B', and 'C'. In addition to the buffer pointer and size, VecDeque has two more integer fields, "start" and "stop", that tell where the data is within the buffer. "start" is the index of the front element, 'A'. "stop" is the index of the gap immediately following the back element, 'E'.)
Figure 16-3. How a VecDeque is stored in memory

Oftentimes, when you need a deque, .push_back() and .pop_front() are the only two methods that you’ll need. The type-associated functions VecDeque::new() and VecDeque::with_capacity(n), for creating queues, are just like their counterparts in Vec. Many Vec methods are also implemented for VecDeque: .len() and .is_empty(), .insert(index, value), .remove(index), .extend(iterable), and so on.

Deques, like vectors, can be iterated by value, by shared reference, or by mut reference. They have the three iterator methods .into_iter(), .iter(), and .iter_mut(). They can be indexed in the usual way: deque[index].

Because deques don’t store their elements contiguously in memory, they can’t inherit all the methods of slices. But if you’re willing to pay the cost of shifting the contents around, VecDeque provides a method that will fix that:

deque.make_contiguous()
Takes &mut self and rearranges the VecDeque into contiguous memory, returning &mut [T].

Vecs and VecDeques are closely related, and the standard library provides two trait implementations for easily converting between the two:

Vec::from(deque)
Vec<T> implements From<VecDeque<T>>, so this turns a deque into a vector. This costs O(n) time, since it may require rearranging the elements.
VecDeque::from(vec)

VecDeque<T> implements From<Vec<T>>, so this turns a vector into a deque. This is also O(n), but it’s usually fast, even if the vector is large, because the vector’s heap allocation can simply be moved to the new deque.

This method makes it easy to create a deque with specified elements, even though there is no standard vec_deque![] macro:

use std::collections::VecDeque;

let v = VecDeque::from(vec![1, 2, 3, 4]);

BinaryHeap<T>

A BinaryHeap is a collection whose elements are kept loosely organized so that the greatest value always bubbles up to the front of the queue. Here are the three most commonly used BinaryHeap methods:

heap.push(value)
Adds a value to the heap.
heap.pop()
Removes and returns the greatest value from the heap. It returns an Option<T> that is None if the heap was empty.
heap.peek()
Returns a reference to the greatest value in the heap. The return type is Option<&T>.
heap.peek_mut()

Returns a PeekMut<T>, which acts as a mutable reference to the greatest value in the heap and provides the type-associated function pop() to pop this value from the heap. Using this method, we can choose to pop or not pop from the heap based on the maximum value:

use std::collections::binary_heap::PeekMut;

if let Some(top) = heap.peek_mut() {
    if *top > 10 {
        PeekMut::pop(top);
    }
}

BinaryHeap also supports a subset of the methods on Vec, including BinaryHeap::new(), .len(), .is_empty(), .capacity(), .clear(), and .append(&mut heap2).

For example, suppose we populate a BinaryHeap with a bunch of numbers:

use std::collections::BinaryHeap;

let mut heap = BinaryHeap::from(vec![2, 3, 8, 6, 9, 5, 4]);

The value 9 is at the top of the heap:

assert_eq!(heap.peek(), Some(&9));
assert_eq!(heap.pop(), Some(9));

Removing the value 9 also rearranges the other elements slightly so that 8 is now at the front, and so on:

assert_eq!(heap.pop(), Some(8));
assert_eq!(heap.pop(), Some(6));
assert_eq!(heap.pop(), Some(5));
...

Of course, BinaryHeap is not limited to numbers. It can hold any type of value that implements the Ord built-in trait.

This makes BinaryHeap useful as a work queue. You can define a task struct that implements Ord on the basis of priority so that higher-priority tasks are Greater than lower-priority tasks. Then, create a BinaryHeap to hold all pending tasks. Its .pop() method will always return the most important item, the task your program should work on next.

Note: BinaryHeap is iterable, and it has an .iter() method, but the iterators produce the heap’s elements in an arbitrary order, not from greatest to least. To consume values from a BinaryHeap in order of priority, use a while loop:

while let Some(task) = heap.pop() {
    handle(task);
}

HashMap<K, V> and BTreeMap<K, V>

A map is a collection of key-value pairs (called entries). No two entries have the same key, and the entries are kept organized so that if you have a key, you can efficiently look up the corresponding value in a map. In short, a map is a lookup table.

Rust offers two map types: HashMap<K, V> and BTreeMap<K, V>. The two share many of the same methods; the difference is in how the two keep entries arranged for fast lookup.

A HashMap stores the keys and values in a hash table, so it requires a key type K that implements Hash and Eq, the standard traits for hashing and equality.

Figure 16-4 shows how a HashMap is arranged in memory. Darker regions are unused. All keys, values, and cached hash codes are stored in a single heap-allocated table. Adding entries eventually forces the HashMap to allocate a larger table and move all the data into it.

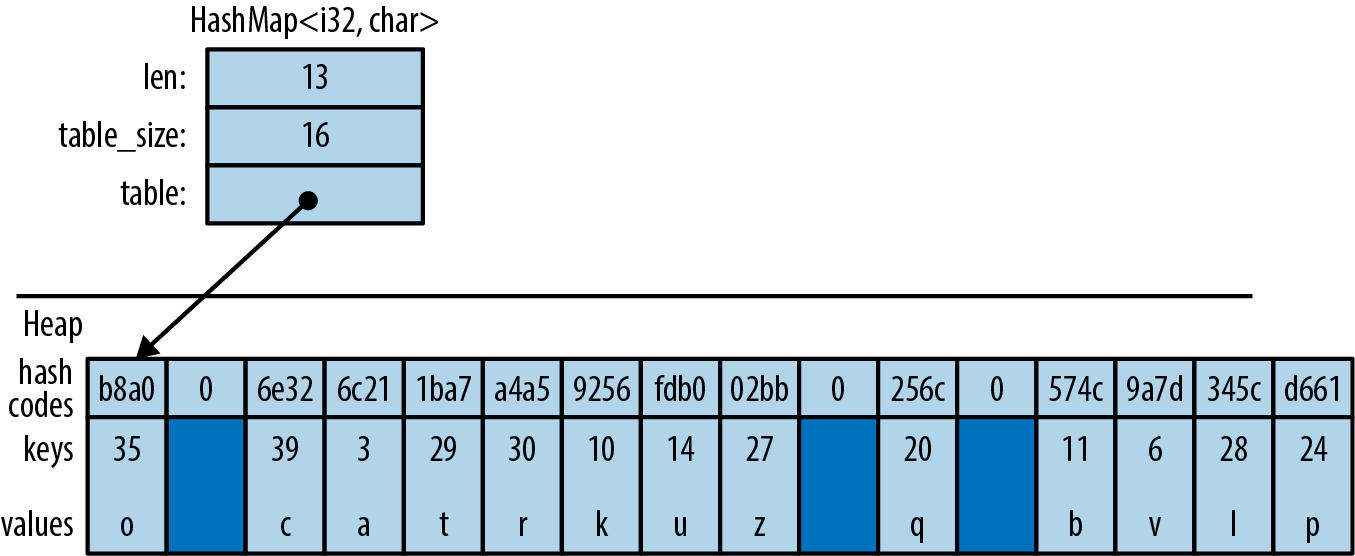
(An illustration of a hash table with 16 slots, 13 of them occupied.)
Figure 16-4. A HashMap in memory

A BTreeMap stores the entries in order by key, in a tree structure, so it requires a key type K that implements Ord. Figure 16-5 shows a BTreeMap. Again, the darker regions are unused spare capacity.

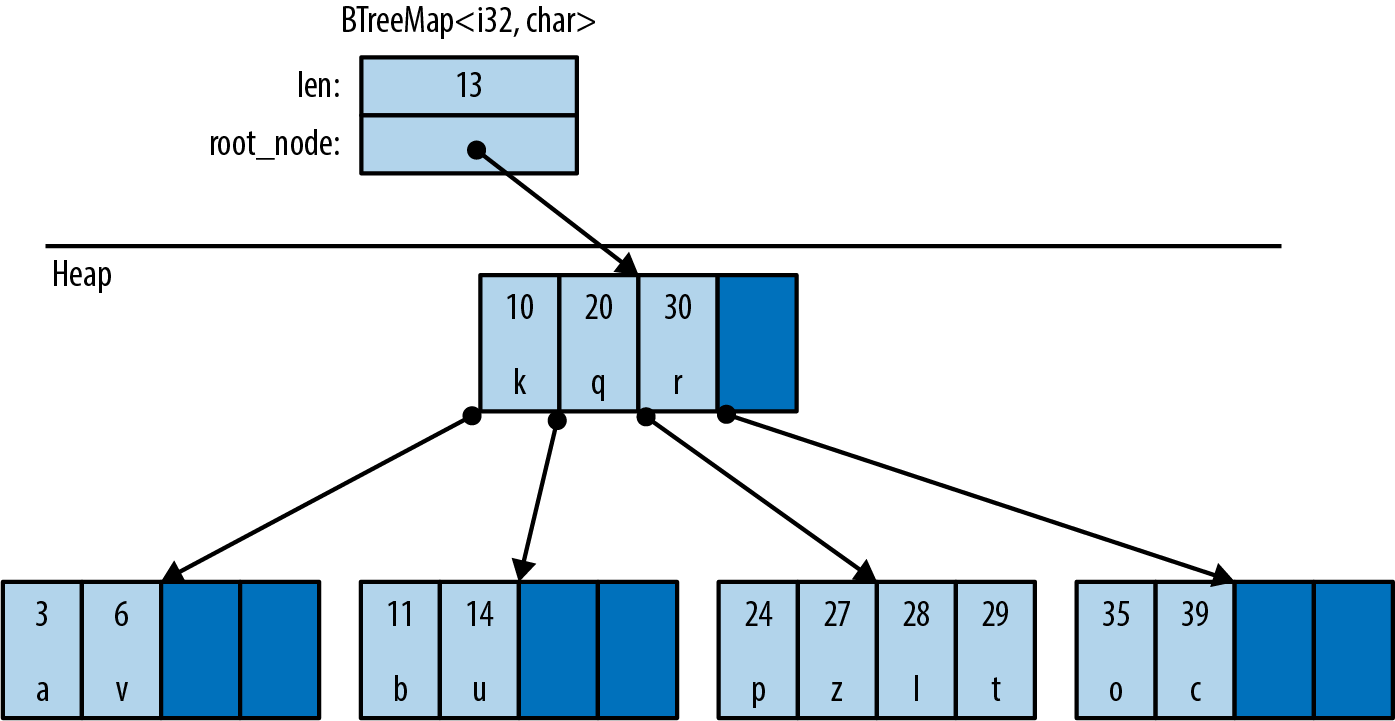
(An illustration of how BTreeMaps are stored in memory. A `BTreeMap`'s data is stored in nodes. Each node holds a limited number of key-value pairs.)
Figure 16-5. A BTreeMap in memory

A BTreeMap stores its entries in nodes. Most nodes in a BTreeMap contain only key-value pairs. Nonleaf nodes, like the root node shown in this figure, also have room for pointers to child nodes. The pointer between (20, 'q') and (30, 'r') points to a child node containing keys between 20 and 30. Adding entries often requires sliding some of a node’s existing entries to the right, to keep them sorted, and occasionally involves allocating new nodes.

This picture is a bit simplified to fit on the page. For example, real BTreeMap nodes have room for 11 entries, not 4.

The Rust standard library uses B-trees rather than balanced binary trees because B-trees are faster on modern hardware. A binary tree may use fewer comparisons per search than a B-tree, but searching a B-tree has better locality—that is, the memory accesses are grouped together rather than scattered across the whole heap. This makes CPU cache misses rarer. It’s a significant speed boost.

There are several ways to create a map:

HashMap::new(), BTreeMap::new()
Create new, empty maps.
iter.collect()
Can be used to create and populate a new HashMap or BTreeMap from key-value pairs. iter must be an Iterator<Item=(K, V)>.
HashMap::with_capacity(n)
Creates a new, empty hash map with room for at least n entries. HashMaps, like vectors, store their data in a single heap allocation, so they have a capacity and the related methods hash_map.capacity(), hash_map.reserve(additional), and hash_map.shrink_to_fit(). BTreeMaps do not.

HashMaps and BTreeMaps have the same core methods for working with keys and values:

map.len()
Returns the number of entries.
map.is_empty()
Returns true if map has no entries.
map.contains_key(&key)
Returns true if the map has an entry for the given key.
map.get(&key)
Searches map for an entry with the given key. If a matching entry is found, this returns Some(r), where r is a reference to the corresponding value. Otherwise, this returns None.
map.get_mut(&key)

Similar, but it returns a mut reference to the value.

In general, maps let you have mut access to the values stored inside them, but not the keys. The values are yours to modify however you like. The keys belong to the map itself; it needs to ensure that they don’t change, because the entries are organized by their keys. Modifying a key in-place would be a bug.

map.insert(key, value)
Inserts the entry (key, value) into map and returns the old value, if any. The return type is Option<V>. If there’s already an entry for key in the map, the newly inserted value overwrites the old one.
map.extend(iterable)
Iterates over the (K, V) items of iterable and inserts each of those key-value pairs into map.
map.append(&mut map2)
Moves all entries from map2 into map. Afterward, map2 is empty.
map.remove(&key)
Finds and removes any entry with the given key from map, returning the removed value, if any. The return type is Option<V>.
map.remove_entry(&key)
Finds and removes any entry with the given key from map, returning the removed key and value, if any. The return type is Option<(K, V)>.
map.retain(test)

Removes all elements that don’t pass the given test. The test argument is a function or closure that implements FnMut(&K, &mut V) -> bool. For each element of map, this calls test(&key, &mut value), and if it returns false, the element is removed from the map and dropped.

Apart from performance, this is like writing:

map = map.into_iter().filter(test).collect();
map.clear()
Removes all entries.

A map can also be queried using square brackets: map[&key]. That is, maps implement the Index built-in trait. However, this panics if there is not already an entry for the given key, like an out-of-bounds array access, so use this syntax only if the entry you’re looking up is sure to be populated.

The key argument to .contains_key(), .get(), .get_mut(), and .remove() does not have to have the exact type &K. These methods are generic over types that can be borrowed from K. It’s OK to call fish_map.contains_key("conger") on a HashMap<String, Fish>, even though "conger" isn’t exactly a String, because String implements Borrow<&str>. For details, see “Borrow and BorrowMut”.

Because a BTreeMap<K, V> keeps its entries sorted by key, it supports an additional operation:

btree_map.split_off(&key)
Splits btree_map in two. Entries with keys less than key are left in btree_map. Returns a new BTreeMap<K, V> containing the other entries.

Entries

Both HashMap and BTreeMap have a corresponding Entry type. The point of entries is to eliminate redundant map lookups. For example, here’s some code to get or create a student record:

// Do we already have a record for this student?
if !student_map.contains_key(name) {
    // No: create one.
    student_map.insert(name.to_string(), Student::new());
}
// Now a record definitely exists.
let record = student_map.get_mut(name).unwrap();
...

This works fine, but it accesses student_map two or three times, doing the same lookup each time.

The idea with entries is that we do the lookup just once, producing an Entry value that is then used for all subsequent operations. This one-liner is equivalent to all the preceding code, except that it does the lookup only once:

let record = student_map.entry(name.to_string()).or_insert_with(Student::new);

The Entry value returned by student_map.entry(name.to_string()) acts like a mutable reference to a place within the map that’s either occupied by a key-value pair, or vacant, meaning there’s no entry there yet. If vacant, the entry’s .or_insert_with() method inserts a new Student. Most uses of entries are like this: short and sweet.

All Entry values are created by the same method:

map.entry(key)

Returns an Entry for the given key. If there’s no such key in the map, this returns a vacant Entry.

This method takes its self argument by mut reference and returns an Entry with a matching lifetime:

pub fn entry<'a>(&'a mut self, key: K) -> Entry<'a, K, V>

The Entry type has a lifetime parameter 'a because it’s effectively a fancy kind of borrowed mut reference to the map. As long as the Entry exists, it has exclusive access to the map.

Back in “Structs Containing References”, we saw how to store references in a type and how that affects lifetimes. Now we’re seeing what that looks like from a user’s perspective. That’s what’s going on with Entry.

Unfortunately, it is not possible to pass a reference of type &str to this method if the map has String keys. The .entry() method, in that case, requires a real String.

Entry values provide three methods to deal with vacant entries:

map.entry(key).or_insert(value)

Ensures that map contains an entry with the given key, inserting a new entry with the given value if needed. It returns a mut reference to the new or existing value.

Suppose we need to count votes. We can write:

let mut vote_counts: HashMap<String, usize> = HashMap::new();
for name in ballots {
    let count = vote_counts.entry(name).or_insert(0);
    *count += 1;
}

.or_insert() returns a mut reference, so the type of count is &mut usize.

map.entry(key).or_default()
Ensures that map contains an entry with the given key, inserting a new entry with the value returned by Default::default() if needed. This only works for types that implement Default. Like or_insert, this method returns a mut reference to the new or existing value.
map.entry(key).or_insert_with(default_fn)

This is the same, except that if it needs to create a new entry, it calls default_fn() to produce the default value. If there’s already an entry for key in the map, then default_fn is not used.

Suppose we want to know which words appear in which files. We can write:

// This map contains, for each word, the set of files it appears in.
let mut word_occurrence: HashMap<String, HashSet<String>> =
    HashMap::new();
for file in files {
    for word in read_words(file)? {
        let set = word_occurrence
            .entry(word)
            .or_insert_with(HashSet::new);
        set.insert(file.clone());
    }
}

Entry also provides a convenient way to modify only extant fields.

map.entry(key).and_modify(closure)

Calls closure if an entry with the key key exists, passing in a mutable reference to the value. It returns the Entry, so it can be chained with other methods.

For instance, we could use this to count the number of occurrences of words in a string:

// This map contains all the words in a given string,
// along with the number of times they occur.
let mut word_frequency: HashMap<&str, u32> = HashMap::new();
for c in text.split_whitespace() {
    word_frequency.entry(c)
        .and_modify(|count| *count += 1)
        .or_insert(1);
}

The Entry type is an enum, defined like this for HashMap (and similarly for BTreeMap):

// (in std::collections::hash_map)
pub enum Entry<'a, K, V> {
    Occupied(OccupiedEntry<'a, K, V>),
    Vacant(VacantEntry<'a, K, V>)
}

The OccupiedEntry and VacantEntry types have methods for inserting, removing, and accessing entries without repeating the initial lookup. You can find them in the online documentation. The extra methods can occasionally be used to eliminate a redundant lookup or two, but .or_insert() and .or_insert_with() cover the common cases.

HashSet<T> and BTreeSet<T>

Sets are collections of values arranged for fast membership testing:

let b1 = large_vector.contains(&"needle");    // slow, checks every element
let b2 = large_hash_set.contains(&"needle");  // fast, hash lookup

A set never contains multiple copies of the same value.

Maps and sets have different methods, but behind the scenes, a set is like a map with only keys, rather than key-value pairs. In fact, Rust’s two set types, HashSet<T> and BTreeSet<T>, are implemented as thin wrappers around HashMap<T, ()> and BTreeMap<T, ()>.

HashSet::new(), BTreeSet::new()
Create new sets.
iter.collect()
Can be used to create a new set from any iterator. If iter produces any values more than once, the duplicates are dropped.
HashSet::with_capacity(n)
Creates an empty HashSet with room for at least n values.

HashSet<T> and BTreeSet<T> have all the basic methods in common:

set.len()
Returns the number of values in set.
set.is_empty()
Returns true if the set contains no elements.
set.contains(&value)
Returns true if the set contains the given value.
set.insert(value)
Adds a value to the set. Returns true if a value was added, false if it was already a member of the set.
set.remove(&value)
Removes a value from the set. Returns true if a value was removed, false if it already wasn’t a member of the set.
set.retain(test)

Removes all elements that don’t pass the given test. The test argument is a function or closure that implements FnMut(&T) -> bool. For each element of set, this calls test(&value), and if it returns false, the element is removed from the map and dropped.

Apart from performance, this is like writing:

set = set.into_iter().filter(test).collect();

As with maps, the methods that look up a value by reference are generic over types that can be borrowed from T. For details, see “Borrow and BorrowMut”.

Whole-Set Operations

So far, most of the set methods we’ve seen are focused on a single value in a single set. Sets also have methods that operate on whole sets:

set1.intersection(&set2)

Returns an iterator over all values that are in both set1 and set2.

For example, if we want to print the names of all students who are taking both brain surgery and rocket science classes, we could write:

for student in &brain_class {
    if rocket_class.contains(student) {
        println!("{}", student);
    }
}

Or, shorter:

for student in brain_class.intersection(&rocket_class) {
    println!("{}", student);
}

Amazingly, there’s an operator for this.

&set1 & &set2 returns a new set that’s the intersection of set1 and set2. This is the binary bitwise AND operator, applied to two references. This finds values that are in both set1 and set2:

let overachievers = &brain_class & &rocket_class;
set1.union(&set2)

Returns an iterator over values that are in either set1 or set2, or both.

&set1 | &set2 returns a new set containing all those values. It finds values that are in either set1 or set2.

set1.difference(&set2)

Returns an iterator over values that are in set1 but not in set2.

&set1 - &set2 returns a new set containing all those values.

set1.symmetric_difference(&set2)

Returns an iterator over values that are in either set1 or set2, but not both.

&set1 ^ &set2 returns a new set containing all those values.

And there are three methods for testing relationships between sets:

set1.is_disjoint(set2)
True if set1 and set2 have no values in common—the intersection between them is empty.
set1.is_subset(set2)
True if set1 is a subset of set2—that is, all values in set1 are also in set2.
set1.is_superset(set2)
This is the reverse: it’s true if set1 is a superset of set2.

Sets also support equality testing with == and !=; two sets are equal if they contain the same values.

Hashing

std::hash::Hash is the standard library trait for hashable types. HashMap keys and HashSet elements must implement both Hash and Eq.

Most built-in types that implement Eq also implement Hash. The integer types, char, and String are all hashable; so are tuples, arrays, slices, and vectors, as long as their elements are hashable.

One principle of the standard library is that a value should have the same hash code regardless of where you store it or how you point to it. Therefore, a reference has the same hash code as the value it refers to, and a Box has the same hash code as the boxed value. A vector vec has the same hash code as the slice containing all its data, &vec[..]. A String has the same hash code as a &str with the same characters.

Structs and enums don’t implement Hash by default, but an implementation can be derived:

/// The ID number for an object in the British Museum's collection.
#[derive(Clone, PartialEq, Eq, Hash)]
enum MuseumNumber {
    ...
}

This works as long as the type’s fields are all hashable.

If you implement PartialEq by hand for a type, you should also implement Hash by hand. For example, suppose we have a type that represents priceless historical treasures:

struct Artifact {
    id: MuseumNumber,
    name: String,
    cultures: Vec<Culture>,
    date: RoughTime,
    ...
}

Two Artifacts are considered equal if they have the same ID:

impl PartialEq for Artifact {
    fn eq(&self, other: &Artifact) -> bool {
        self.id == other.id
    }
}

impl Eq for Artifact {}

Since we compare artifacts purely on the basis of their ID, we must hash them the same way:

use std::hash::{Hash, Hasher};

impl Hash for Artifact {
    fn hash<H: Hasher>(&self, hasher: &mut H) {
        // Delegate hashing to the MuseumNumber.
        self.id.hash(hasher);
    }
}

(Otherwise, HashSet<Artifact> would not work properly; like all hash tables, it requires that hash(a) == hash(b) if a == b.)

This allows us to create a HashSet of Artifacts:

let mut collection = HashSet::<Artifact>::new();

As this code shows, even when you implement Hash by hand, you don’t need to know anything about hashing algorithms. .hash() receives a reference to a Hasher, which represents the hashing algorithm. You simply feed this Hasher all the data that’s relevant to the == operator. The Hasher computes a hash code from whatever you give it.

Using a Custom Hashing Algorithm

The hash method is generic, so the Hash implementations shown earlier can feed data to any type that implements Hasher. This is how Rust supports pluggable hashing algorithms.

A third trait, std::hash::BuildHasher, is the trait for types that represent the initial state of a hashing algorithm. Each Hasher is single use, like an iterator: you use it once and throw it away. A BuildHasher is reusable.

Every HashMap contains a BuildHasher that it uses each time it needs to compute a hash code. The BuildHasher value contains the key, initial state, or other parameters that the hashing algorithm needs every time it runs.

The complete protocol for computing a hash code looks like this:

use std::hash::{Hash, Hasher, BuildHasher};

fn compute_hash<B, T>(builder: &B, value: &T) -> u64
    where B: BuildHasher, T: Hash
{
    let mut hasher = builder.build_hasher();  // 1. start the algorithm
    value.hash(&mut hasher);                  // 2. feed it data
    hasher.finish()                           // 3. finish, producing a u64
}

HashMap calls these three methods every time it needs to compute a hash code. All the methods are inlineable, so it’s very fast.

Rust’s default hashing algorithm is a well-known algorithm called SipHash-1-3. SipHash is fast, and it’s very good at minimizing hash collisions. In fact, it’s a cryptographic algorithm: there’s no known efficient way to generate SipHash-1-3 collisions. As long as a different, unpredictable key is used for each hash table, Rust is secure against a kind of denial-of-service attack called HashDoS, where attackers deliberately use hash collisions to trigger worst-case performance in a server.

But perhaps you don’t need that for your application. If you’re storing many small keys, such as integers or very short strings, it is possible to implement a faster hash function, at the expense of HashDoS security. The fnv crate implements one such algorithm, the Fowler–Noll–Vo (FNV) hash. To try it, add this line to your Cargo.toml:

[dependencies]
fnv = "1.0"

Then import the map and set types from fnv:

use fnv::{FnvHashMap, FnvHashSet};

You can use these two types as drop-in replacements for HashMap and HashSet. A peek inside the fnv source code reveals how they’re defined:

/// A `HashMap` using a default FNV hasher.
pub type FnvHashMap<K, V> = HashMap<K, V, FnvBuildHasher>;

/// A `HashSet` using a default FNV hasher.
pub type FnvHashSet<T> = HashSet<T, FnvBuildHasher>;

The standard HashMap and HashSet collections accept an optional extra type parameter specifying the hashing algorithm; FnvHashMap and FnvHashSet are generic type aliases for HashMap and HashSet, specifying an FNV hasher for that parameter.

Beyond the Standard Collections

Creating a new, custom collection type in Rust is much the same as in any other language. You arrange data by combining the parts the language provides: structs and enums, standard collections, Options, Boxes, and so on. For an example, see the BinaryTree<T> type defined in “Generic Enums”.

If you’re used to implementing data structures in C++, using raw pointers, manual memory management, placement new, and explicit destructor calls to get the best possible performance, you’ll undoubtedly find safe Rust rather limiting. All of those tools are inherently unsafe. They are available in Rust, but only if you opt in to unsafe code. Chapter 22 shows how; it includes an example that uses some unsafe code to implement a safe custom collection.

For now, we’ll just bask in the warm glow of the standard collections and their safe, efficient APIs. Like much of the Rust standard library, they’re designed to ensure that the need to write unsafe is as rare as possible.